Skip to main content

Research Highlight: Efficient Analysis of Large Climate Datasets

By Eli Woodard

Involved group of researchers: Alejandro N. Flores, Kachinga Silwimba, and other members of the research team at Boise State University.

Researcher Kachinga Silwimba explained, “Climate change is an increasingly critical issue that demands immediate attention from the global community. In light of this, combining climate model emulation with the Empirical Orthogonal Functions (EOF) methodology represents a promising approach for comprehending and anticipating changes in climate variability patterns”.

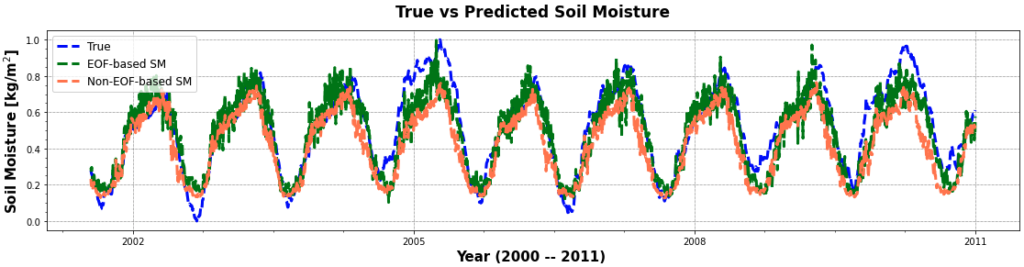
Silwimba, under the supervision of PI Alejandro N. Flores, is working on developing a computational method that combines climate model emulation and empirical orthogonal functions (EOF) analysis. This novel approach aims to reduce computational costs associated with traditional methods, thereby making it more feasible to perform more extensive climate analyses with increased accuracy and reduced time.

The team uses climate model simulations from the Community Land Model Version 5 at the National Center for Atmospheric Research (NCAR). To develop emulators and perform the EOF analysis, they rely on Python and bash Scripting, statistical software packages. Given the size of the climate datasets, which can be quite large, access to High-Performance Computing (HPC) resources is also necessary for the efficient completion of the project.

Silwimba explained, “One of the primary challenges I encountered during my research project was the initial unfamiliarity with the Computing cluster (R2 and Borah), which posed difficulties in the initial setup and management of the system. Thankfully, I was fortunate enough to receive guidance from Katie Murenbeeld, a member of my lab (Lab for Ecohydrological and Forecasting) here at Boise State University. Katie provided valuable assistance in navigating and troubleshooting the cluster’s operations, allowing me to efficiently conduct my research,”.

Our research approach involves applying the EOF method to identify the dominant patterns of variability in the climate data. This technique entails calculating the eigenvalues and eigenvectors of the climate data’s covariance matrix or using the Singular Value Decomposition (SVD) method to decompose the data into empirical orthogonal function modes, which represent the spatial distributions and principal components, which also represent the temporal distributions.

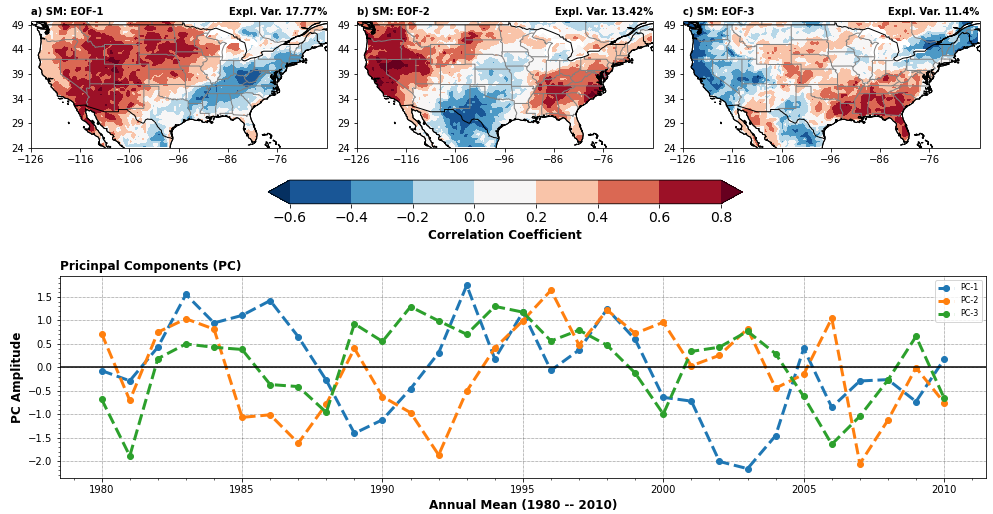
Maps and graphs
Figure 1: At the top, there are three maps of the United States side by side, each representing different Empirical Orthogonal Functions (EOF) labeled as a) SM: EOF-1, b) SM: EOF-2, and c) SM: EOF-3. These maps are color-coded to show correlation coefficients ranging from -0.6 to 0.8, with blue shades indicating negative correlations and red shades indicating positive correlations. The percentage of explained variance by each EOF mode is listed as 17.7% for EOF-1, 13.42% for EOF-2, and 11.4% for EOF-3. Below the maps, there’s a line graph with the title “Principal Components (PC)” showing three lines representing PC1, PC2, and PC3, each with a different color and style (solid, dashed, and dotted). The X-axis of the graph represents years from 1980 to 2010, and the Y-axis represents the amplitude of the PCs, ranging from -2.0 to 1.5. The lines fluctuate over the years, depicting how each principal component’s influence varies over time. The caption explains that the Empirical Orthogonal Functions (EOF) analysis was conducted on soil moisture data collected between January 1980 to December 2010. The analysis revealed that the first three EOF modes explain 42.59% of the total variance observed during the study period. This indicates the significance of these modes in characterizing the spatial distribution of soil moisture over time.
Graph
Figure 2: The figure displays three lines representing different datasets over time, specifically from the years 2000 to 2011. The lines are color-coded as follows: Blue dashed line labeled “True” represents the actual measured soil moisture. Green solid line labeled “EOF-based SM” represents soil moisture predicted by a model that uses Empirical Orthogonal Functions (EOF). Orange dashed line labeled “Non-EOF-based SM” represents soil moisture predicted by a model that does not use EOF. The Y-axis on the left side of the graph measures soil moisture in kilograms per square meter (kg/m^2) and ranges from 0 to 1.0. The X-axis represents the years from 2000 to 2011. All three lines follow a similar pattern of peaks and troughs, indicating the seasonal or periodic variation in soil moisture over time. The green EOF-based line and the orange non-EOF-based line closely track the blue actual soil moisture line, though there are places where they deviate slightly, suggesting differences in the accuracy of the two predictive models when compared to the actual data.

 

Silwimba is currently engaged in several related research projects, including investigating the impact of various parameters on Climate Land Model version 5 simulations using empirical orthogonal functions (EOFs). Additionally, he is exploring the combination of self-organizing maps (Neural Networks) with EOFs to assess the influence of these parameters on the performance of the Climate Land Model (CLM).

Silwimba concluded, “Machine learning-based emulation methods, designed to mimic complex climate models, can significantly reduce the computational costs associated with running these models. By providing faster and more accurate predictions, these methods allow researchers to explore a broader range of climate scenarios and make better-informed policy decisions. Moreover, they can make climate projections more accessible to policymakers and the general public, bridging the gap between climate modeling research and the broader community. This can ultimately contribute towards a more sustainable future by increasing public awareness and understanding of the potential impacts of climate change”.

To find out how Research Computing can help with a project, email researchcomputing@boisestate.edu.