MODELING THE EFFECT OF POINT DEFECTS IN PEROVSKITES
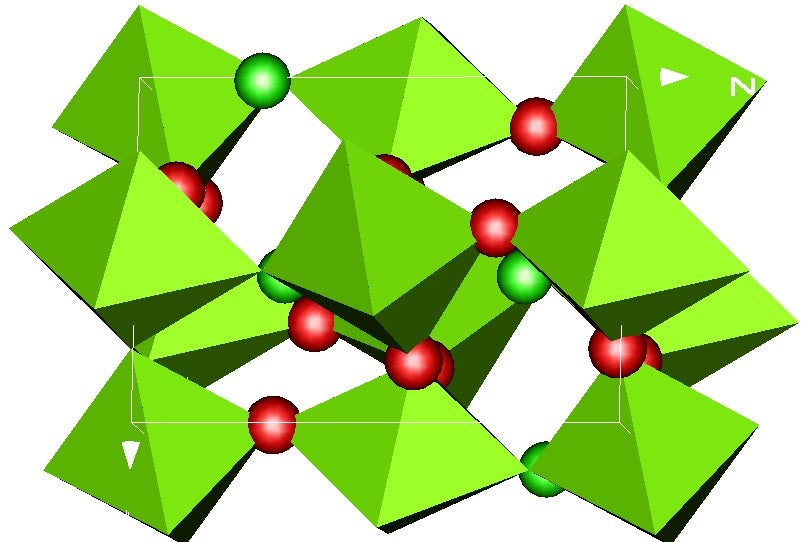
Perovskites
Many electroceramics are based on or related to the perovskite crystal structure. The generic perovskite oxide formula is generally written as ABO3. In the ideal cubic form, the A site is coordinated to 12 anions to form cuboctahedral coordination polyhedra. The B site is coordinated to six anions, forming octahedra. The anions are coordinated to just two B site cations, as the four nearest A-site cations are about 41% further away. The anion octahedra are corner shared, which is a key feature of all perovskites.
Perovskites abound both in nature and in the laboratory, and their wide compositional range renders a variety of useful properties such that perovskites are encountered in applications as disparate as electroceramics, superconductors, refractories, catalysts, magnetoresistors, and proton conductors. They are also of interest for use as substrates or buffer layers for compound semiconductor heteroepitaxy. The design of such advanced materials requires an understanding of the relationship between chemical composition and crystal structure.
Applications
As of 2022 There are over 300 million smart phone subscribers in the USA, and 4.6 billion cell phone users worldwide, making the cellular phone one of the fastest-selling consumer items in history and the most widely spread technology on the planet. There are three times as many mobile phones than PCs of any kind in the world and more mobile phones than cars. There are over twice as many mobile phone users as internet users, and more mobile phone users than people with a credit card. Twice as many people use SMS text messaging worldwide than use e-mail, with 75,000 messages sent every second in the USA!
Microwave resonators are used extensively in telecommunications equipment, including cellular telephones and satellite links, and are at the heart of this multi-billion dollar market. Oxide ceramics are critical elements in these devices, and three properties are important in determining their usefulness as a dielectric resonator. First, the material must have a high dielectric constant (εr) to enable size reduction, the size of a microwave circuit being proportional to εr-½. Second, a high quality factor Q (low tanδ) means fine frequency tunability and more channels within a given band. Third, these ceramic components play a crucial role in compensating for frequency drift because of their low temperature coefficients of resonant frequency (τf). Optimizing all these properties in a single material is not a trivial problem, and a full understanding of the crystal chemistry of such ceramics is paramount to future development. Many perovskite-structured ceramic materials are known to have useful microwave dielectric properties, with potential applications in the mobile telecommunications market.
The effect of defects
In this study, a solid-state processing method is used to synthesize single-phase perovskite ceramics with engineered defect concentrations. Powder samples are characterized via X-ray diffraction. The resulting products are then uniaxially pressed and sintered for microstructural analysis. The ultimate goal is to develop a predictive model, based solely on composition, for the effect of point defects on the structure and, by extension, dielectric properties of perovskites.
Point defects like vacancies can have a profound effect on the structure of perovskite ceramics, but the exact mechanisms by which they do this are unclear. There is some evidence in a variety of perovskite systems that A-site vacancies increase the average A-O bond distance due to mutual electrostatic repulsion of anions across the negatively-charged vacant site, which increases as the number of vacancies increases. A predictive model for the pseudocubic lattice constant which accounts for A-site vacancies and the ionic radii in their correct coordinations (XII, VI, and II for the A, B, and X species respectively) has been recently developed and shown to work adequately in several systems.